Radix Trees
How IntMap Works
Tikhon Jelvis
Graphs
Functional Graphs
FGL
⇒
Data.IntMap
PATRICIA
Practical Algorithm to Retrieve Information Coded in Alphanumeric
Other Uses
Merging
Prefix Operations
- all keys, sorted
- read by prefix
- update by prefix
Tries
Retrieval
lookup “b”
b = 1
lookup “bab”
b
lookup “bab”
b → a
lookup “bab”
b → a → b = 7
Prefixes
every key starting with “ba”
b
b → a
b → a
Tries
retrieve key character by character
Binary Trie
Bit-by-Bit
Paths
two keys: 00011, 00001
Path Compression
two keys: 00011, 00001
Path Compression
Path Compression
fully compressed radix tree
Data.IntMap
binary trie with path compression
Data.IntMap
Leaf(path, key, value)Branch(path, children)Empty
Data.IntMap
type Prefix = Int
type Mask = Int
data IntMap a =
Branch !Prefix
!Mask
!(IntMap a) !(IntMap a)
| Leaf !Prefix a
| Empty
lookup
lookup _ Empty = Nothing
lookup k (Leaf k' v)
| k == k' = Just v
| otherwise = Nothing
lookup
lookup k (Branch prefix control l r)
| getPrefix k control /= prefix = Nothing
| k .&. control == 0 = lookup k l
| otherwise = lookup k r
getPrefix k control =
key .&. complement ((control `shiftL` 1) - 1)
Binary Trie
- binary: “bit-by-bit”
- binary: “two children”
Span
n bits = 2ⁿ children
Space vs Height
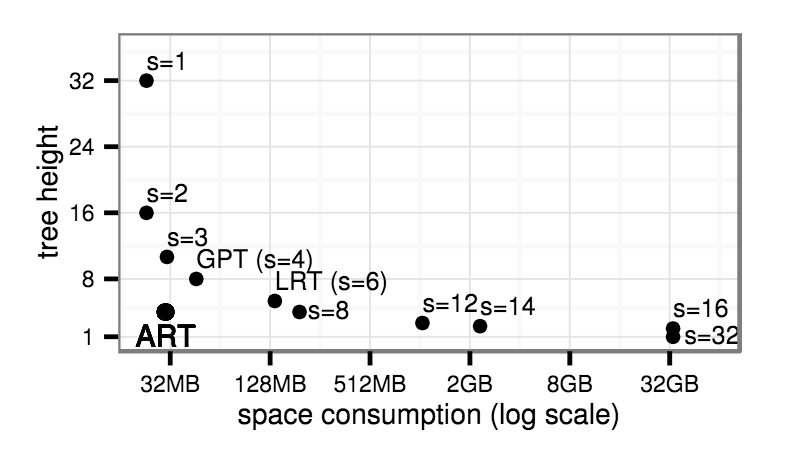
from ART paper
Adaptive Radix Tree
Adaptive Radix Tree
256 children (byte at a time)
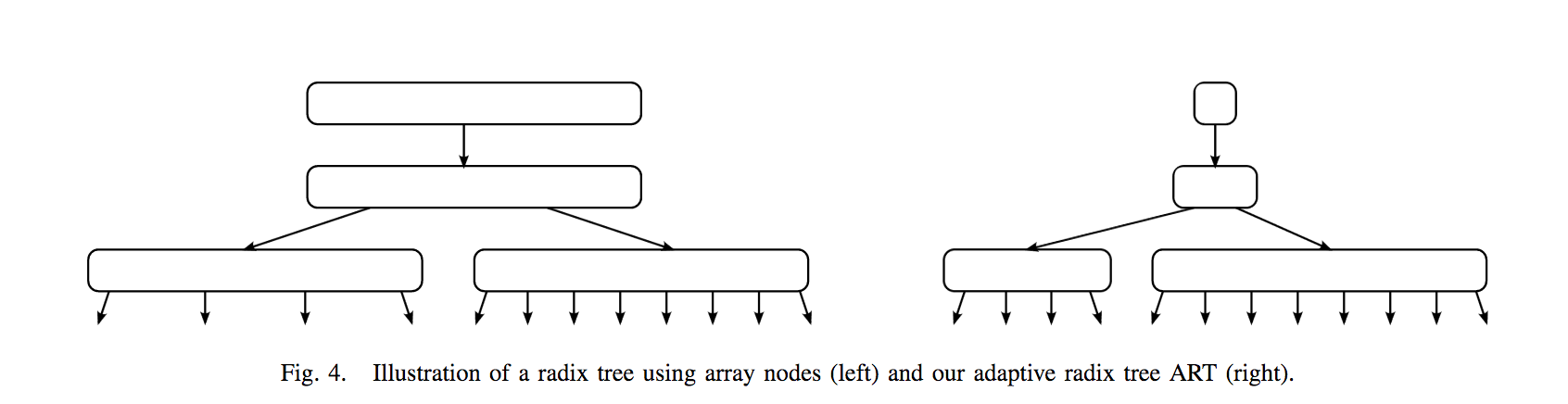
Nodes
Adaptive Radix Tree
data ART a = Empty
| Leaf !Key a
| Node !Mask !Prefix !(Children a)
Nodes
type Chunk = Word8
type Chunks = UArray Chunk Chunk
type Values a = Array Chunk a
type Size = Word8
data Children a =
N4 !Size !Chunks !Values
| N16 !Size !Chunks !Values
| N48 !Size !Chunks !Values
| N256 !Size !(Array Chunk (Maybe a))
Persistent Adaptive Radix Trees?
- Java version
- good fit for Haskell?
Tries
- sorted keys
- prefix operations
- merging
Data.IntMap
- binary trie
- path compression
Beyond IntMap
- different spans
- adaptive radix trees